Тригонометрические формулы

Основные тригонометрические тождества

sin² α + cos² α = 1
tg α · ctg α = 1
tg α = sin α ÷ cos α
ctg α = cos α ÷ sin α
1 + tg² α = 1 ÷ cos² α
1 + ctg² α = 1 ÷ sin² α

Формулы сложения

sin (α + β) = sin α · cos β + sin β · cos α
sin (α - β) = sin α · cos β - sin β · cos α
cos (α + β) = cos α · cos β - sin α · sin β
cos (α - β) = cos α · cos β + sin α · sin β
tg (α + β) = (tg α + tg β) ÷ (1 - tg α · tg β)
tg (α - β) = (tg α - tg β) ÷ (1 + tg α · tg β)
ctg (α + β) = (ctg α · ctg β + 1) ÷ (ctg β - ctg α)
ctg (α - β) = (ctg α · ctg β - 1) ÷ (ctg β + ctg α)

Формулы двойного угла

cos 2α = cos² α - sin² α
cos 2α = 2cos² α - 1
cos 2α = 1 - 2sin² α
sin 2α = 2sin α · cos α
tg 2α = (2tg α) ÷ (1 - tg² α)
ctg 2α = (ctg² α - 1) ÷ (2ctg α)

Формулы тройного угла

sin 3α = 3sin α - 4sin³ α
cos 3α = 4cos³ α - 3cos α
tg 3α = (3tg α - tg³ α) ÷ (1 - 3tg² α)
ctg 3α = (3ctg α - ctg³ α) ÷ (1 - 3ctg² α)

Формулы понижения степени

sin² α = (1 - cos 2α) ÷ 2
sin³ α = (3sin α - sin 3α) ÷ 4
cos² α = (1 + cos 2α) ÷ 2
cos³ α = (3cos α + cos 3α) ÷ 4
sin² α · cos² α = (1 - cos 4α) ÷ 8
sin³ α · cos³ α = (3sin 2α - sin 6α) ÷ 32

Переход от произведения к сумме

sin α · cos β = ½ (sin (α + β) + sin (α - β))
sin α · sin β = ½ (cos (α - β) - cos (α + β))
cos α · cos β = ½ (cos (α - β) + cos (α + β))

Формулы перехода от суммы к произведению тригонометрических функций

Ключевые слова: тригонометрия, синус, косинус, тангенс, котангенс, формулы перехода о суммы к произведению

Рассмотрим формулу 2sinXcosY=sin(X+Y)+sin(X-Y)
Обозначим в правой части этой формулы X+Y через , а X-Y через  .
Складывая и вычитая равенства X+Y=  и X-Y=  ,
находим, что X=2+, Y=2−
подставляя эти выражения в левую часть формулы и читая формулу справа налево, получаем окончательно:
sin+sin=2sin2+cos2−
Подставляя в только что полученную формулу -   вместо  ,
получаем sin−sin=2sin2−cos2+.

Аналогично можно вывести все остальные формулы

cos+sin=2sin(4)=2cos(4) 

 Основные тригонометрические тождества 

Выражение тригонометрических функций через одну из них того же аргумента 

(выбор знака перед корнем зависит от того, в какой четверти находится угол )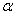

     Через :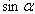 

  Через :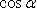

     Через :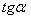

   Через :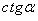

   Преобразование суммы тригонометрических функций 

где 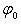 - угол, для которого

в частности, 

 Преобразование произведения тригонометрических функций в сумму

  Тригонометрические функции двойного и тройного аргумента

 Тригонометрические функции половинного аргумента 

(выбор знака зависит от того, в какой четверти находится угол )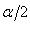

  Выражение тригонометрической функции через тангенс половинного аргумента 

  Преобразование степеней синуса и косинуса